|
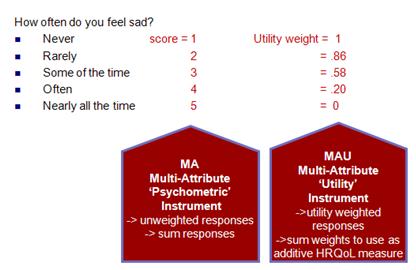
Scoring - Psychometric (unweighted) or Utility (weighted)? As a 'utility' measure: When utilities are computed, these instruments can provide dimension scores and an overall index of the health state utility which can be used in economic evaluations, and specifically, cost-utility analysis requiring the computation of quality-adjusted life years (QALYs). The ‘utilities’ are, in effect, preference weights and final utility scores should reflect peoples’ preferences more accurately than unweighted aggregates. The following example question about feeling sad demonstrates the two ways of scoring:
Please choose the appropriate instrument, statistical package and instructions, then download the algorithms to calculate your scores.
Utility algorithms (weighted)
Unweighted algorithms
NB: Correction to the AQoL-6D algorithms
AQoL-6D for adults versus AQol-6D ADOLESCENT Utility Scores The aqol.com.au website now recommends the scoring algorithm reproduced from model 6 for adults and the algorithm from model 1 for adolescents. This implies that adolescent scores calculated from model 1 should not, in principle, be compared with adult scores calculated from model 6 (or model 9, the original model recommended in Richardson et al 2007). Model 1 scores may be obtained from the formula: AQoL-6D (model 1) = [AQoL-6D (Multiplicative)]0.59
This may be further adjusted to obtain the adolescent scores described in Moodie et al. (2010).
|
|